به نام دانای برحق
مقدمه
سلام یاده زمانی که دانشگاه بودم سر کلاس ریاضی کاربردی خیلی حال می کردم چون نکات جدیدی رو درک می کردم یکی از درس های ریاضی کاربردی مختصات قطبی بودش که شاید تا الان بیش از ۲۰ مرتبه استفاده شده ازش برام.
در مختصات دکارتی شما محدودیت این رو دارید که نمیتونید اشکال دایره وار به راحتی ترسیم کنید شما فرض کنید می خواهید یه سری نقطه چین ترسیم کنید که به شکل دایره ای باشه برای محاسبه تو مختصات دکارتی تقریبا با نظرم درست کردنش غیر ممکن هستش حال آنکه سیستم دیجیتالی سیستم عامل هایی که ما باهاشون کار می کنیم از ما فقط مختصات دکارتی رو می پذیرند روی همین حساب ما باید یه کار دیگه کنیم اون زمان هستش مختصا قطبی به درد ما میخوره.
ما در این قسمت از دو زبان یکی زبان تحت وب کلاینت استفاده می کنیم javascript و یه زبان تحت ویندوز Delphi
مختصات قطبی و تفاوت آن با دکارتی
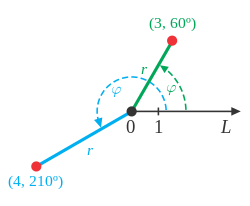
به زبان ساده ما با بیان تفاوت بهتر میتونیم این مسائله رو روشن کنیم ما برای آدرس دهی در روش دکارتی به دو نقطه نیاز داریم x و y که معادل طول و ارتفاع هستش خوب حالا متخصات قطبی تفاوت دارد و نحوه آدرسی بر اساس این است که مرکز صفحه مختصات میشود محور کار می برای آدرس دهی ما یک فاصله با یک زاویه میدهیم مثلا فاصله ۲۱۰ پیکسل با زاویه ۴۵ درجه از مبدا مختصات میشه آدرس دهی ما اما به نقل از ویکی پدیا این شکلی میتونیم تعریف کنیم:
دستگاه مختصات قطبی، یک دستگاه مختصات دوبعدی است که در آن مکان هر نقطه، با فاصلهٔ آن تا مرکز مختصات (r) و زاویه بین خط رسمشده از مرکز به آن نقطه و محور طول، (θ) مشخص میشود. این دستگاه در سه بعد به دستگاه مختصات استوانهای و دستگاه مختصات کروی تبدیل میشود.
اولین استفادههای مشابه که به ایجاد کنونی این دستگاه انجامیدهاست توسط ابوریحان بیرونی انجام شد.
خب حالا یه نمونه تغییرات پر مختصات قطبی و درکاتی میبینیم در تصویر زیر با فومولش تا شما با این نوع متخصات آشنا بشید:
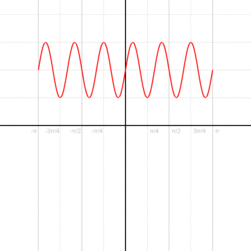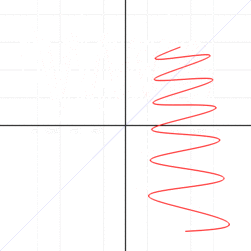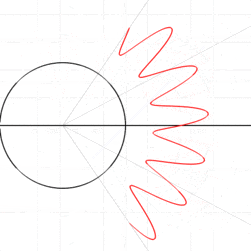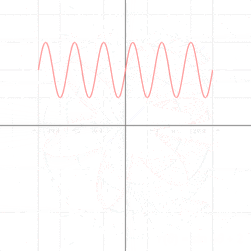
و این یک شکل دیگه اس که شکل حلزونی رو تو مخصات قطبی پیاده سازی کرده و با یه فرمول یک خطی این خطوط رو ترسیم کرده اما در دکارتی نمیشه به سادگی این کار رو کرد مثلا فرمول زیر میشه:
r(φ) = φ / ۲π for۰ < φ < 6π

تبدیل مختصات قطبی به دکارتی
حال آنکه ما از مزایای این مختصات مطلع شدیم بر این بر می آییم که که چطور مختصات قطبی رو تبدیل به مختصات دکارتی کنیم برای این کار ریاضیدانان یک فرمول ارائه کردن:
x = r * sin(φ) y = r * cos(φ)
خب برای این کار شما فرمول مورد نظر قطبی مختصات ترسیم رو باید مدام بدست بیاورید و سپس در این فرمول به دکارتی تبدیل و رسم نمایید.
تابع تبدیل مختصات قطبی به مختصات دکارتی در دلفی و js
در زبان js ما یه سری توابع زیر مجموعه Math داریم که به کارمون میادش بنابراین تابع به شکل زیر میشود:
function Pol2Dec(r,teta){
var result = new Array();
result.x = r * Math.sin(teta);
result.y = r * Math.cos(teta);
return result;
}
نحوه استفاده:
console.log(Pol2Dec(7,45));
پاسخ رو میتونید تو کنسول مرورگر تماشا کنید که معادل: [x: ۵.۹۵۶۳۲۴۶۷۱۷۳۸۸۲۴, y: ۳.۶۷۷۲۵۳۹۲۱۷۲۴۱۰۶] میباشد.
خب میریم حالا به سراغ زبان Primary خودمون یعنی دلفی عزیز 😀 در دلفی از قبل باید یه تایپ تعریف کنیم تا نقطه در تابع قابل بازگشت باشه به و یونت math استفاده شود و تابع به شکل زیر میشود:
type Point = array[1..2] of float; // x = 1 ; y = 2 function Pol2Dec(r,teta:float):Point; begin result[1] = r * sin(teta); result[2] = r * cos(teta); end;
و نحوه استفاده به صورت زیر هستش:
....
var
decp: Point;
begin
decp = Pol2Dec(7,45);
showmessage('x: '+floattostr(decp[1]));
showmessage('y: '+floattostr(decp[2]));
end;
امیدوارم مفدی وافع شده باشه در ادامه در مورد موارد گرافیکی بیشتر صحبت می کنیم.

دیدگاهتان را بنویسید لغو پاسخ